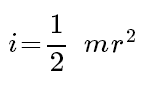The purpose of this lab is studying about inertia and the parallel theorem.
First of all, we cut a half circle from a paper.Therefore, we need to predict the inertial first by calculation, and determine the real inertial later by getting the angular acceleration.
Phys4AF14 jhu
2014年12月11日星期四
2014年11月27日星期四
Mass-Spring Oscillations Lab
In this lab, we were going to find factors effecting period of the spring oscillation. Professor wolf asked us to be two team, and each team had four groups to measure spring constants of different springs and their mass.
First of all, we need to measure all spring constant of them. We determined the original length of spring S1, and put a 0.05 kg mass on the spring and measure the length of spring S2. Thus, the spring constant is (0.05kg*9.8m/s^2)/(S2-S1).
spring constant and mass:
1. 2.44 N/m 9.7 g
2. 6.5 N/m 11.1 g
3. 23.3 N/m 27.7 g
4. 18.52 N/m 19.9 g
In my group,our spring is the first one in the list.We hanged 106 g mass on the spring and make it rock. And then, we use computer to collect its motivation.
From the graph, we can find the period 1.6 s.
After four groups finishing the experiment, we showed the data to each other.
spring spring constant mass mass add to the 100 g hanging mass period
1 2.44 N/m 9.7 g 6 g 1.6 s
2 6.5 N/m 11.1 g 5 g 0.814 s
3 23.3 N/m 27.7 g 0 g 0.42 s
4 18.52 N/m 19.9 g 3 g 0.47 s
From this table, we made a graph to directly show the relationship.
Conclusion,as the mass being bigger, the period will be smaller.
As the spring constant being bigger, the period will be smaller as well.
And what we predict,the period will be smaller when the spring constant being bigger, but the period will be bigger when the mas increases, so I confused about this.
If the value of spring constant were 5 % off, the period will be 2.34% increases.
A high value of spring constant spring means a greater force in Newton's second law, F = ma. For a given mass, that means a greater acceleration so the mass will move faster and, therefore, complete its motion quicker or in a shorter period.
Newton's second law, F = ma or a = F/m , tells us that a larger mass will have a smaller acceleration (for the same force) so that a greater mass will simply move slower and, therefore, take a longer time to complete its motion.
First of all, we need to measure all spring constant of them. We determined the original length of spring S1, and put a 0.05 kg mass on the spring and measure the length of spring S2. Thus, the spring constant is (0.05kg*9.8m/s^2)/(S2-S1).
spring constant and mass:
1. 2.44 N/m 9.7 g
2. 6.5 N/m 11.1 g
3. 23.3 N/m 27.7 g
4. 18.52 N/m 19.9 g
In my group,our spring is the first one in the list.We hanged 106 g mass on the spring and make it rock. And then, we use computer to collect its motivation.
From the graph, we can find the period 1.6 s.
After four groups finishing the experiment, we showed the data to each other.
spring spring constant mass mass add to the 100 g hanging mass period
1 2.44 N/m 9.7 g 6 g 1.6 s
2 6.5 N/m 11.1 g 5 g 0.814 s
3 23.3 N/m 27.7 g 0 g 0.42 s
4 18.52 N/m 19.9 g 3 g 0.47 s
From this table, we made a graph to directly show the relationship.
Conclusion,as the mass being bigger, the period will be smaller.
As the spring constant being bigger, the period will be smaller as well.
And what we predict,the period will be smaller when the spring constant being bigger, but the period will be bigger when the mas increases, so I confused about this.
If the value of spring constant were 5 % off, the period will be 2.34% increases.
A high value of spring constant spring means a greater force in Newton's second law, F = ma. For a given mass, that means a greater acceleration so the mass will move faster and, therefore, complete its motion quicker or in a shorter period.
Newton's second law, F = ma or a = F/m , tells us that a larger mass will have a smaller acceleration (for the same force) so that a greater mass will simply move slower and, therefore, take a longer time to complete its motion.
Ruler and clay
The purpose of this lab is studying about the maximum height after the ruler impacts and sticks to the clay can reach.
Data:
mass of ruler 0.088 kg
mass of clay 0.025 kg
the length of ruler: 1 m
the distance between the hole on ruler and one end side of ruler: 0.99 m
the inertia of ruler rotating around hole is 0.02846 kg*m^2
And then, we need to know the angular speed of the ruler before it stick to the clay, so we assume there is not friction between the ruler and the hole.
According to the conversation of angular momentum, we use below function to find the angular speed of the ruler and clay after collision.
And then,we are able to get the high:
The expected height is 0.3344 m.
However, in the experiment, we only got 0.135 m.
Conclusion, the expected data and real data are not quite same, but we have expected it because when the ruler hit the clay that stick to a rod, stickiness made the ruler slow down too much.
Conservation of Linear and Angular Momentum
In this experiment, we will study about the conservation between a object's linear velocity and its angular momentum. Therefore, we will try doing the experiment to expect the angular speed of the disk after the ball impact the disk in order to to in order to study the angular momentum and linear momentum of a ball in collision.
First of all, professor set the equipment to know the velocity of the ball(0.0247 kg) before collision as below picture shows:
First of all, professor set the equipment to know the velocity of the ball(0.0247 kg) before collision as below picture shows:
We determined the distance between end of track and the ground is 0.955 m and the distance of horizontal travel of the ball is 0.552 m.
From this function, we can get the time it take, and we can make horizontal distance divide the time to get the velocity. And then, we get 1.1824 m/s.
After getting the velocity and the mass of the ball, we are able to know the linear momentum of the ball.
Next section is determining the angular momentum of the ball, so we need to know the disk's angular velocity and inertia after collision. However, we decide to find the inertia first. For finding the inertia, we will use a string that attended to a hanging mass wrapping around the top pulley.And then, let it drop down and measure the angular acceleration.
angular acceleration: 5.6365 rad/s^2
top pulley's radius: 0.025 m
mass of ball: 0.0247 kg
And we use this function to get the inertia:
After we substitute data:
And then, we are able to find the angular speed after collision:
Thus, we expect the angular speed is 1.957 rad/s.
But the real angular speed is 1.775 rad/s.
Conclusion: the reason why the expect one is bigger than real one is the friction and the disk is not perfect friction-less. However, this lab helps us recognize the conservation of linear and angular momentum.
2014年11月26日星期三
Finding the moment of inertia of uniform triangle about its center
The purpose of this lab is determining the moment of inertia of a uniform triangle about its center of mass. Therefore, we will use computer to determine the real inertia of the object, use formula to figure out the inertia, and compare them.
As the picture shows below, we set the triangle on a holder and disk. The upper disk floats on a cushion of air, so there is not fiction when the disk rotates.A string is wrapped around a pulley on top of and attached to the disk, and go over a freely-rotating pulley to a hanging mass.
We measured data:
hanging mass: 0.025 kg
radius of top pulley: 0.025 m
After substitute data:
angular acceleration of the entire disk with triangle:
average angular acceleration: 2.0225 rad/s^2
After substitute, we get the inertia is 3.012*10^-3 kg*m^2
Therefore, we were able to get the triangle inertia:
I1= 3.012*10^-3 kg*m^2 - 2.78*10^-3 kg*m^2= 2.328*10^-4 kg*m^2
And we also try to measure another inertia of triangle in different direction, so we turned the triangle 90 degrees:
the acceleration of triangle after turning: 1.8365 rad/s^2
After substitution, we get the inertia I2 is 5.3952*10^-4 kg*m^2
Thus, for different direction of the same object, their inertia are different.
And then, we need to calculate the inertia with formula. We know the inertia of triangle that around one side of it: I=bh^3/12
We also get the b=0.098 m and h=0.149 m, and the distance d from side to center of mass is 0.149/3 m.
We apply parallel-axis theorem to this question: Icm=I-md^2.
However, for the both of experiments, the inertia is not quite equate to what we got from experiment.
As the picture shows below, we set the triangle on a holder and disk. The upper disk floats on a cushion of air, so there is not fiction when the disk rotates.A string is wrapped around a pulley on top of and attached to the disk, and go over a freely-rotating pulley to a hanging mass.
We measured data:
hanging mass: 0.025 kg
radius of top pulley: 0.025 m
However, first of all, we have to find the inertia 1 of disk without the object and the inertia 2 of the disk with object, and use inertia 2 subtract the inertia 1 in order to get the inertia of the object.
From this function, we can substitute numbers to get the inertia. And then, the only number we need to know is angular accelerations.
angular acceleration of empty disk:
average angular acceleration: 2.191 rad/s^2After substitute data:
Inertia of empty disk is 2.78*10^-3 kg*m^2
angular acceleration of the entire disk with triangle:
After substitute, we get the inertia is 3.012*10^-3 kg*m^2
Therefore, we were able to get the triangle inertia:
I1= 3.012*10^-3 kg*m^2 - 2.78*10^-3 kg*m^2= 2.328*10^-4 kg*m^2
And we also try to measure another inertia of triangle in different direction, so we turned the triangle 90 degrees:
the acceleration of triangle after turning: 1.8365 rad/s^2
After substitution, we get the inertia I2 is 5.3952*10^-4 kg*m^2
Thus, for different direction of the same object, their inertia are different.
And then, we need to calculate the inertia with formula. We know the inertia of triangle that around one side of it: I=bh^3/12
We also get the b=0.098 m and h=0.149 m, and the distance d from side to center of mass is 0.149/3 m.
We apply parallel-axis theorem to this question: Icm=I-md^2.
However, for the both of experiments, the inertia is not quite equate to what we got from experiment.
2014年11月18日星期二
Moment of Inertia
The purpose of this lab is studying about inertia of a large metal disk.
First of all, we set up a large metal disk on a central shaft, and made a appropriate measurements of the rotating part of the apparatus and determined its moment of inertia.
And then, for judging the result is correct or not, we connected this apparatus to a 500 g dynamics cart. The cart would drag the string that connected around the disk with constant force in order to give a constant angular acceleration to the disk. Later, we let the cart roll down an inclined track for a distance of one meter, and we could determine the time it took so that we could use those data to figure out the physical moment of inertia.
In the first section, we need to know the mass and radius of the disk to get the inertia, and we measured the radius of the disk in two parts. The bigger part's radius is 0.03 cm, and the smaller part's radius is 1.67 cm. For the mass, we determined the bigger one is 4.08 kg, and the smaller one is 0.749 kg. After this, from below equation, we got the smaller inertia is 0.0001044 kg*m^2, and the bigger one is 0.020115 kg*m^2, so the total inertia is 0.0202 kg*m^2.
Let radius times the acceleration to get the angular acceleration is -2.1208 rad/s^2, for friction torque, we let the angular acceleration times inertia, and we got -0.042841 N*m.
First of all, we set up a large metal disk on a central shaft, and made a appropriate measurements of the rotating part of the apparatus and determined its moment of inertia.
And then, for judging the result is correct or not, we connected this apparatus to a 500 g dynamics cart. The cart would drag the string that connected around the disk with constant force in order to give a constant angular acceleration to the disk. Later, we let the cart roll down an inclined track for a distance of one meter, and we could determine the time it took so that we could use those data to figure out the physical moment of inertia.
In the first section, we need to know the mass and radius of the disk to get the inertia, and we measured the radius of the disk in two parts. The bigger part's radius is 0.03 cm, and the smaller part's radius is 1.67 cm. For the mass, we determined the bigger one is 4.08 kg, and the smaller one is 0.749 kg. After this, from below equation, we got the smaller inertia is 0.0001044 kg*m^2, and the bigger one is 0.020115 kg*m^2, so the total inertia is 0.0202 kg*m^2.
And then, we need to know the friction torque of the disk, so we let the disk rotate and stop by itself for measuring the slowing angular acceleration by computer and camera.
From this graph, we found the linear acceleration is -0.2106 m/s^2.Let radius times the acceleration to get the angular acceleration is -2.1208 rad/s^2, for friction torque, we let the angular acceleration times inertia, and we got -0.042841 N*m.
After we measure the angle of the track and the ground, we substitute all data to above equation, so we got the cart acceleration is 0.152 m/s^2.
For one meter inclined track, we got the time is 2.565 s.
However, our disk was not perfect to rotating and it made noise sound, so the time it took was longer the 2.565 s. But we found a good way to make it better is making the angle between ground and track to be bigger, and the error would be smaller even though it was still not perfect.
2014年11月1日星期六
Angular acceleration: Part 1
The purpose of this lab is discovering what are factors affect the angular acceleration of a object.
As the picture shows, we set up those devices to study some factors such as the mass of disk, the force dragging the disk,and the diameter of the torque pulley.
However, we need to measure them first.
data:
the diameter and mass of the top steel disk: 126.2 mm 1361 g
the diameter and mass of the bottom steel disk: 126.2 mm 1348 g
the diameter and mass of the top aluminum disk: 126.2 mm 464.5 g
the diameter and mass of the smaller torque pulley: 24.9 mm 10 g
the diameter and mass of the larger torque pulley: 49.8 mm 36.3 g
the mass of the hanging mass supplied with the apparatus: 24.5 g
After we measured those data,we need to determine different angular acceleration of different situations with the device.
In those picture, we can get two angular accelerations of each situation, and we calculate the average of two angular accelerations.
grams actually hanging torque pulley disk a
1 24.5 g small steel 1.1375 rad/s
2 50 g small steel 2.293 rad/s
3 75 g small steel 3.4625 rad/s
4 24.5 g large steel 2.213 rad/s
5 24.5 g large aluminum 6.2135 rad/s
6 24.5 g large steel 1.1777 rad/s
conclusion:
conclusion:
From this table,we can see that the angular acceleration will increases as the force dragging the disk, the angular acceleration will increases as the diameter of torque pulley is bigger, and the angular acceleration will increases as the mass of the object is decreasing.
订阅:
评论 (Atom)