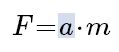Work and Energy

In this lab, we were going to study about work and energy.

we went out side to calculate the amount of work for walking up in height h with stair and how much work we use to drag an object up the same height. We will also calculate the power as well.

We had three steps we need to do in lab.

1.drag a bag with mass of 9 kg and record the time we used.

2.walk up to the same height and record the time we used.

3.run up to the same height and record the time we used.

From the equation, we can calculate the work to apply to finish our work.

W=Fd

First,we need to know the height of the floor.

we measure each stair height is 0.17m, and there are 26 steps, so the total height is 4.42m.

And then, we measured the time for dragging object, walking, and running.

dragging: 15.45s

walking: 16.13s

running: 4.77s

dragging:

Work:

(9kg) (9.8m/s^2)(4.42m) = 389.844 joules

Power:

work / 15.45 second = 25.23 watts

walking:

Bag on pulley:

(95kg)(9.8m/s^2)(4.42m) =  4115.02 joules

Power:

work / 16.13 seconds = 255.11 watts

running:

Bag on pulley:

(95kg)(9.8m/s^2)(4.42m) =  4115.02 joules

Power:

work / 4.77 seconds = 862.68 watts

centripetal acceleration as a function of angular speed

In this lab, we were going to study about the angular velocity and angular acceleration.

As the picture show, we would rotate the plate and collect the period with timer. And then, we got following graph.

From the graph, we can see when period decreases, the acceleration is increasing.

Moreover, we know the equation:

w=2Pi/T

Therefore, when angular speed increases, the acceleration is increasing.

And we also found the graph about angular acceleration and angular velocity^2 gives a positive slope of 0.1493 as liner function. 

It shows that both of them are proportional to each other, and because it matters with radius of the turn table because a=r*w^2. a is acceleration and w is angular velocity, r is the slope of the graph.

Frind relationship between angular velocity and angle of a conical pendulum

In the lab, our purpose is finding the relationship between the angle of conical pendulum and angular velocity.And this is the picture showing about lab:

And then, we use the ruler to measure l ans L.
l: 0.6 m L: 0.67 m H(total height) : 2.3 m
However, what should we do for measure the angular velocity? And what can we measure the angle during the object is rotating? We will get not accurate number if we only use angle measure tool and angular velocity measure tool. Thus,we can use equation to instead it to  measure the angle and angular velocity.

Angular velocity = 2*Pi/period

Thus, after measuring data, we got those number:

1. T1=3.968s h1=0.5m
2. T2=3.288s h2=0.628m
3. T3=2.953s h3=0.762m
4. T4=2.698s h4=0.955m
5. T5=2.514s h5=1.066m
6. T6=2.205s h6=1.14m
7. T7=1.99s  h7=1.425m
8. T8=1.85s  h8=1.487m

From those number, we use equations to get the graph:

Now, the goal of this lab is finding the relationship, so we made some equations:

divide both side with m:

Because the r is changing with the angle, so we wrote the equation between r and angle:

we apply those two equations, and we can got:

So we use Excel to get the angular velocity by the angle:

From this graph, we can figure out that theory w and real w are similar, so the equation about angle and angular velocity is correct.

Modeling Friction Forces

In this lab, we study about friction of object and figure out coefficient of static friction. And we built 4 different model about friction of object.

1.Put a wooden black on the table, tie a string to the block and connect to water cup over a pulley at the end of the track.And then, we put water to the cup patiently until the block finally starts to slide to edge of table.Record the mass of the cup and water required to get block to start to move.And we add 3 times wooden block and record them to record their mass of wooden block and mass of water.

 The record :

After this, we plug all data into computer to create the graph:

So that, we can the coefficient of static friction between table and block is 

0.2188.

2.drag the block in constant speed by motion sensor which is connected to the block, and we get the graph from Labpro:

And this graph gives us the average kinetic friction force between the block and the track.

After we measure those blocks' mass, we create the table to record mass of block and normal force.

      mass(kg)      normal force(N)   friction(N)

1.  0.11          1.078              0.3177
2.  0.236         2.3131             0.6187
3.  0.295         2.89               0.852
4.  0.45          4.411              1.3

we model sliding friction as being proportional to the normal force, and speed of the moving object. That is, we create a function:

Fkinetic=K*N=>K=Fkinetic/N

we get the number K is 0.2947. 

3.We make a slope with the metal track and put the motion sensor at the bottom of the track, and then let a wooden block to slide down to bottom from top.And we can record the acceleration with computer and sensor, show in picture:

from this graph, we are able to apply the equation to get net force:

and the net force is equal to sin(a)*mg-Ffriction so we can get:

=>

divide the m

=>

the a=0.8527m/s^2,angle a=20degrees, so we get k=0.2807

4.we make a slope, connect the block which is on slope to a mass over pulley, and make the angle between slope and horizontal table to be just make the mass can drag the block to move.
And now, we know the mass is 0.15kg,angle is 21.5degree,block is 160kg, and acceleration is 0.545m/s^2 with measuring.
we create a equation:

and we can get k is 0.5539

measure density of metal

In this lab, our goal is figuring out the uncertainty of values.
In the first part, we were going to measure 3 different metals' length, diameter, and mass in order to get the density with its uncertainty.

And then, we get:

    metal         length        diameter         mass            density

1. steel      5.00+-0.01 cm  1.26+-0.01 cm  48.9+=0.1 g      7.6 g/cm^3
2. copper     5.14+-0.01 cm  1.28+-0.01 cm  58.4+=0.1 g      8.8 g/cm^3
3. brass      4.80+-0.01 cm  1.60+-0.01 cm   80.0+=0.1 g     8.3 g/cm^3

From the equation for density:

And then, we take the natural logarithm of each side we get:

=>

1. steel 
   
2. copper
   
3. brass
   

This,we can get those metals' density with their uncertainty:

1. steel:  7.6+-0.15 g/cm^3
2. copper: 8.8+-0.16 g/cm^3
3. brass:  8.3+-0.12 g/cm^3

And, there is next lab to determine the mass of object by measuring two angles and those forces of two strings.

All of first, we focus on the y size of the object.

and then, we focus on the x size of the object.

The data we measure about force on strings and angles:

F1=7.5+-0.5N

F2=7.0+-0.5N

a1=46degree+-1degree

a2=50degree+-1degree

plug those data to equation.

And we can get the force from equation

is 1.0976+-0.015N

Lab 4 Trajectories

In this lab, we were going to predict the impact point of a ball on an inclined board with our understanding of projectile motion.So we need to set up a model to make the ball launching in same direction and speed.
As what picture shows:

And then, we need to tape a carbon paper to the floor about where the ball landed. After this, we launched the ball five times from the same high as before and verify that the ball lands in virtually the same place each time.

Now, because we need to calculate the velocity of the ball, when the ball launches, we need to measure the height of the ball falling, the distance of the ball lands from the table's edge.

With hanging a plumb bob, we also get:

the height of the bottom of the ball when it launches: 0.94 m

the distance of where the ball lands from the table's edge: 0.755 m

=>velocity:

we already known the distance, but we did not the time it falling.

Thus,  from

Vo= 0 m/s, g= -9.8 m/s^2 =>

=>

And,we plug the time and distance into equation:

In this lab, our goal is predicting the impact point of ball on an inclined board. And we have known the Vo and angle of the inclined board.

For predicting impact, we had to create two equation to describe the path of falling ball and the inclined board.

Falling ball:

inclined board:

After solving this two function, we can predict the point (x,y) where the ball will impact the board.And we can get the distance

In experiment, we place a board so that it touched the end of table and floor, and attach a piece of carbon paper to where the ball may impact to board. Finally, find the point and measure the distance, and we found the theoretical value for d is bigger than experimental one, but they are almost same.